정렬 알고리즘
이전에 면접때 컨테이너에 간한 질문을 많이 받았다고 적은적이 있는거 같다. 컨테이너처럼 많이 물어봤던게 알고리즘들이었고, 그중에서 정렬 알고리즘을 꾀 많이 질문받았다. 그중에 기초적이면서 가장 많이 물어본다는 소문의 정렬 알고리즘들에 대해 포스팅해본다.
선택정렬
- 시간 복잡도 : O(n^2) 공간 복잡도 : O(n)
- 현재 위치에 들어갈 자리를 선택해 정렬하는 방식
- 로직
- 제일 앞에서 부터, 배열값 중 가장 작은 값을 찾음
- 찾은 가장 작은값을 현재 인덱스와 교체
- 위 과정 반복
- 코드 예시

삽입정렬
- 현재 위치에서 아래 배열들을 비교하여 찾아들어갈 위치를 찾아 그 위치에 삽입하는 방식
- 시간 복잡도 : 최악 O(n^2), 이미 정렬된 경우 O(n) 공간 복잡도 : O(n)
- 로직
- 첫번째가 아닌 두번째 인덱스부터 시작, 비교 인덱스는 현재 인덱스의 -1
- 비교 인덱스와 별도로 저장해둔 삽입을 위한 값을 비교
- 삽입을 위한값이 더 작을 경우 들어갈 자리를 -1 씩 감소
- 삽입 변수가 더 크면 비교 인덱스의+1 자리에 값을 삽입
- 코드 예시
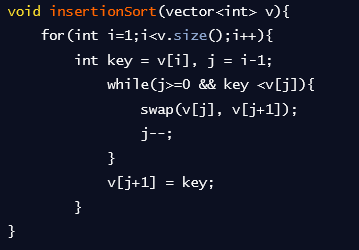
버블정렬
- 연속된 두개의 값들을 비교하여 정한 기준(오름, 내림차순)의 값을 교체하는 방식
- 시간 복잡도 : O(n^2) 공간 복잡도 : O(n)
- 로직
- 현재 인덱스와 바로 다음 인덱스를 비교
- 정한기준에 따라 비교 인덱스가 작거나 크면 교체
- 정한기준에 따라 비교 인덱스가 크거나 작으면 교체하지 않고 다음 연속된 두개로 넘어감
- 이를 전체 배열의 크기 - 현재까지 순환한 바퀴 수 만큼 반복
- 코드 예시
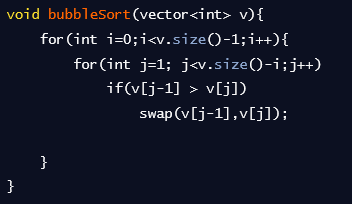
병합정렬
- 분할 정복방식으로 설계됨. 큰 문제를 반씩 쪼개 문제를 해결해 나가는 방식
- 시간 복잡도 : O(n*log n)
- 로직 과정(분할)
- 현재 배열을 반으로 나눈다
- 각각의 시작위치와 끝 위치를 받아 중간 지점을 찾는다
- 이 과정을 나뉜 배열의 크기가 1이하 일때까지 반복한다
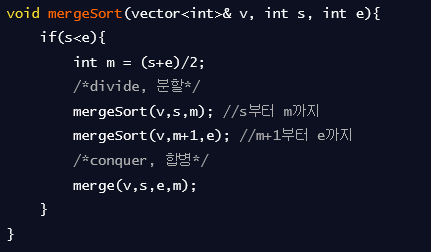
- 로직 과정(합병)
- 나눈 배열의 크기를 비교하고 각각의 현재 인덱스를 가정
- 현재 인덱스중 하나는 나뉜배열중 하나의 시작 위치를, 나머지 현재 인덱스에는 다른 배열의 시작 위치를 지정
- 각각 현재위치에 있는 값들을 비교하고 기준에 따라 알맞은 값을 새로운 배열의 시작 위치부터 저장
- 저장된 값의 원래 위치를 하나씩 증가시키며 각 배열의 끝에 도달할때까지 반복
- 최종적으로 완성된 임시 배열의 값을 원래 배열에 저장

퀵 정렬
- 합병 정렬과 마찬가지로 분할 정복을 이용하여 정렬을 수행 피봇이라는 기준을 설정하여 해당 피봇보다 작은값은 왼쪽 큰값은 오른쪽으로 보내는 방식
- 시간 복잡도 : O(n*log n), 최악(이미 정렬된 배열의 경우) O(n^2) 공간 복잡도 : O(n)
- 로직
- 피봇을 하나 정한다 (일반적으로 맨앞, 맨뒤, 전체의 중간값, 랜덤 값)
- 분할 전에 왼쪽 배열을 저장할 변수와 오른쪽 배열의 인덱스를 저장할 변수를 지정(L, R)
- L에는 피봇보다 작은 인덱스를 R에는 피봇보다 큰 인덱스의 값을 저장
- 분할된 두개의 리스트에 대해 재귀적 호출(혹은 반복)을 통해 이 과정을 반복
- 코드 예시
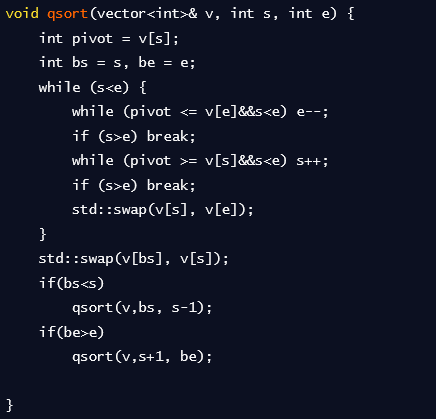
힙 정렬
- 힙 트리를 이용한 알고리즘 최소 힙 구성 : 오름 차순 최대 힙 구성 : 내림 차순
- 시간 복잡도 : O(n*lon n)
- 로직
- N개의 노드에 대한 완전 이진트리를 구성(왼쪽에서 오른쪽으로 단말 노드를 채운 트리, h-1 까진 포화 이진트리)
- 부모노드가 자식노드 보다 큰 트리(최대 힙) 부모노드가 자식노드보다 작은 트리(최소 힙)
- 힙에 대하여 삭제 연산을 수행하여 삭제한 원소를 배열의 마지막 자리에 배치
- 나머지 노드에 대하여 힙 트리 재구성
- 모든 노드가 삭제될때까지 반복
- 코드 예시
